En oversigt over ydeevne for regulære udtryk i Java
1. Oversigt
I denne hurtige vejledning viser vi, hvordan motoren til mønstermatchning fungerer. Vi præsenterer også forskellige måder at optimere på regelmæssige udtryk i Java.
For en introduktion til brugen af regelmæssige udtrykhenvises til denne artikel her.
2. Den mønster-matchende motor
Det java.util.regex pakken bruger en type mønster-matchende motor kaldet a Ikke-bestemmende Endelig Automaton (NFA). Det overvejes ikke-bestemmende fordi mens man prøver at matche et regulært udtryk på en given streng, kan hvert tegn i input kontrolleres flere gange mod forskellige dele af det regulære udtryk.
I baggrunden bruger ovennævnte motor backtracking. Denne generelle algoritme forsøger at udtømme alle muligheder, indtil den erklærer fiasko. Overvej følgende eksempel for bedre at forstå NFA:
"tra (vel | ce | de) m"Med input Snor “rejse“, Vil motoren først kigge efter“tra”Og find det med det samme.
Derefter prøver den at matche “vel”Startende fra det fjerde tegn. Dette vil matche, så det vil gå fremad og prøve at matche “m“.
Det stemmer ikke overens, og af den grund går det tilbage til det fjerde tegn og søger efter “ce“. Igen svarer dette ikke, så det går tilbage til fjerde position og prøver med “de“. Denne streng matcher heller ikke, og så går den tilbage til det andet tegn i inputstrengen og prøver at søge efter en anden “tra“.
Med den sidste fiasko returnerer algoritmen fiasko.
Med det enkle sidste eksempel måtte motoren bakke flere gange, mens han prøvede at matche input Snor til det regulære udtryk. På grund af det, det er vigtigt at minimere den mængde backtracking, det gør.
3. Måder at optimere Regulære udtryk
3.1. Undgå rekompilering
Regulære udtryk i Java er samlet til en intern datastruktur. Denne samling er den tidskrævende proces.
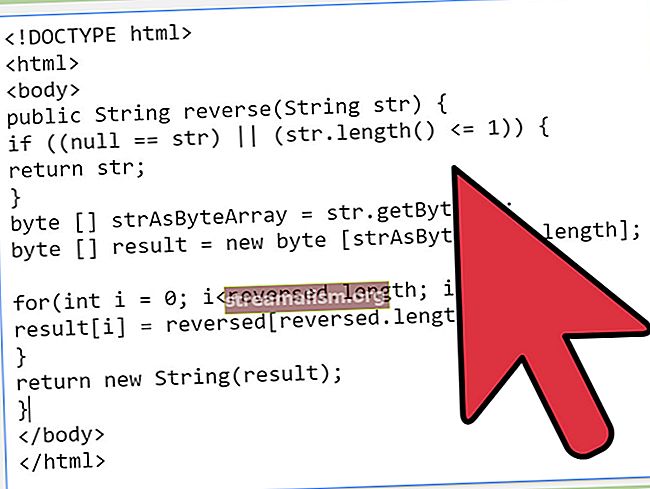
Hver gang vi påberåber os String.matches (String regex) metode, kompileres det angivne regulære udtryk:
hvis (input.matches (regexPattern)) {// gør noget}Som vi kan se, kompileres regex-udtrykket hver gang tilstanden evalueres.
For at optimere er det muligt først at kompilere mønsteret og derefter oprette et Matcher at finde tilfældighederne i værdien:
Mønster mønster = Mønster.kompil (regexPattern); for (Stringværdi: værdier) {Matcher matcher = pattern.matcher (værdi); hvis (matcher.matches ()) {// gør noget}}Et alternativ til ovenstående optimering er at bruge det samme Matcher eksempel med sin Nulstil() metode:
Mønster mønster = Mønster.kompil (regexPattern); Matcher matcher = pattern.matcher (""); for (strengværdi: værdier) {matcher.reset (værdi); hvis (matcher.matches ()) {// gør noget}}På grund af det faktum, at Matcher er ikke trådsikker, skal vi være forsigtige med brugen af denne variation. Det kan sandsynligvis være farligt i scener med flere tråde.
For at opsummere, i enhver situation, hvor vi er sikre på, at der kun er en bruger af Matcher når som helst, er det OK at genbruge det med Nulstil. For resten er det nok at genbruge det forud kompilerede.
3.2. Arbejde med alternativ
Som vi lige tjekkede i det sidste afsnit, kunne den utilstrækkelige brug af alternationer være skadelig for ydeevnen. Det er vigtigt at placere muligheder, der er mere tilbøjelige til at ske foran, så de kan matches hurtigere.
Vi er også nødt til at udtrække fælles mønstre mellem dem. Det er ikke det samme at sige:
(rejse | handel | spor)End:
tra (vel | de | ce)Sidstnævnte er hurtigere, fordi NFA vil prøve at matche “tra”Og vil ikke prøve nogen af alternativerne, hvis den ikke finder det.
3.3. Optagelse af grupper
Hver gang vi er ved at fange grupper, pådrager vi os en mindre tidsstraf.
Hvis vi ikke har brug for at fange teksten i en gruppe, bør vi overveje brugen af ikke-fangende grupper. I stedet for at bruge “(M)", brug venligst "(?: M)“.
4. Konklusion
I denne hurtige artikel besøgte vi kort hvordan NFA arbejder. Vi fortsatte derefter med at undersøge, hvordan vi kan optimere udførelsen af vores regulære udtryk ved at kompilere vores mønstre og genbruge en Matcher.
Endelig påpegede vi et par overvejelser, som vi skal huske på, mens vi arbejder med vekslinger og grupper.
Som sædvanlig kan den fulde kildekode findes på GitHub.